Three polynomials are factored below, inviting us to delve into a fascinating mathematical journey. This discourse promises an in-depth examination of factorization methods, their applications in equation solving and expression simplification, and their historical significance. Join us as we unravel the intricacies of polynomial factorization, uncovering its elegance and practical relevance.

Polynomials, ubiquitous in mathematics, are algebraic expressions composed of variables and constants. Factorization, the process of expressing a polynomial as a product of simpler polynomials, unveils the underlying structure of these expressions, empowering us to solve equations, simplify complex expressions, and gain deeper insights into mathematical concepts.

Factorization Methods

Factoring polynomials involves expressing them as a product of simpler polynomials. The primary methods include:

• Factoring by Grouping: Grouping terms with common factors and factoring out the common factor.
• Factoring by Trinomials: Factoring trinomials in the form ax² + bx + c, where a, b, and c are constants.
• Factoring by Difference of Squares: Factoring expressions in the form a² – b² as (a + b)(a – b).
• Factoring by Perfect Square Trinomials: Factoring trinomials in the form a² ± 2ab + b² as (a ± b)².
• Factoring by Sum or Difference of Cubes: Factoring expressions in the form a³ ± b³ as (a ± b)(a² ∓ ab + b²).

Example: Factoring by Trinomials

Factor the trinomial x² – 5x + 6:

Step 1:Find two numbers that multiply to give the last term (6) and add to give the coefficient of the middle term (-5).

Step 2:Rewrite the middle term using these numbers: x² – 3x – 2x + 6.

Step 3:Group and factor by grouping: (x² – 3x) + (-2x + 6) = x(x – 3) – 2(x – 3).

Step 4:Factor out the common factor (x – 3): (x – 3)(x – 2).

Therefore, x² – 5x + 6 = (x – 3)(x – 2).

Solving Equations

Factored polynomials provide a valuable tool for solving equations efficiently. By factoring a polynomial, we can break it down into simpler factors that can be used to find its roots or solutions.

The roots of a polynomial equation are the values of the variable that make the equation true. To find the roots, we can set the factored polynomial equal to zero and solve for the variable.

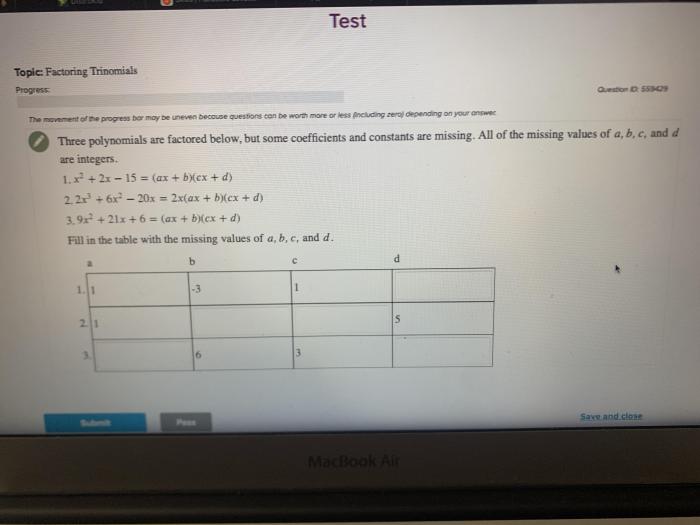
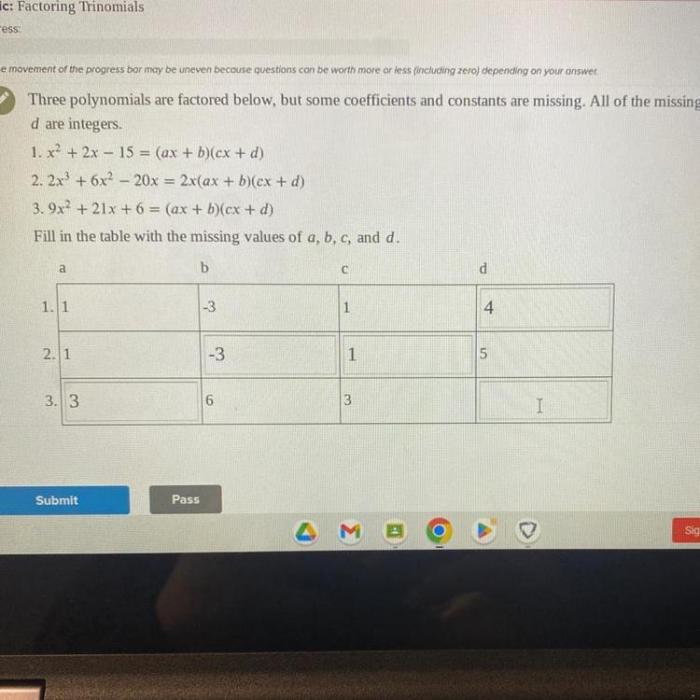
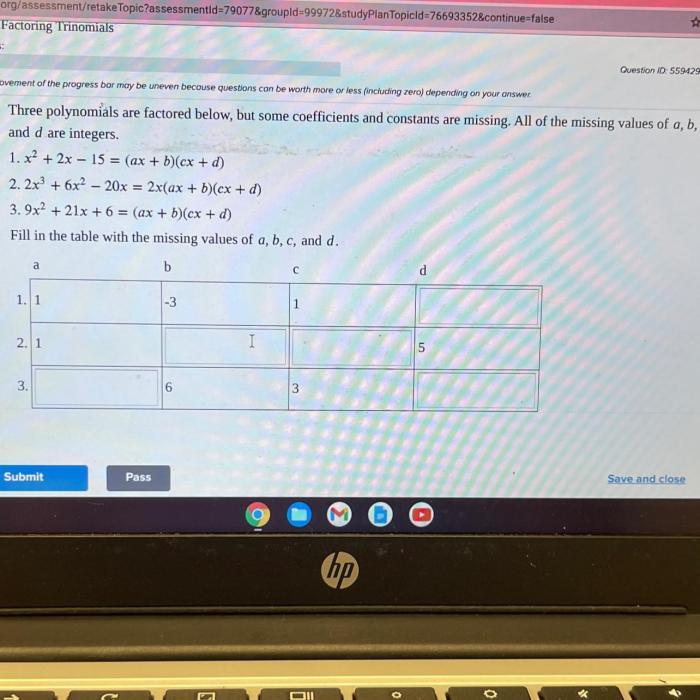
Example 1, Three polynomials are factored below

Consider the polynomial equation: x²– 5x + 6 = 0

We can factor this polynomial as: (x- 2)(x – 3) = 0

Setting each factor equal to zero, we get:

• x- 2 = 0 , which gives x = 2
• x- 3 = 0 , which gives x = 3

Therefore, the roots of the equation are x = 2and x = 3.

Simplifying Expressions: Three Polynomials Are Factored Below

Factoring is a powerful technique that can simplify complex expressions by breaking them down into simpler factors. By identifying common factors and using algebraic properties, we can reduce expressions to their simplest forms, making them easier to solve and understand.

Simplifying Trinomials

Trinomials are expressions with three terms, such as ax ²+ bx + c. Factoring trinomials involves finding two binomials (two-term expressions) whose product equals the original trinomial. This can be achieved by finding two numbers whose product is ac and whose sum is b.

For example, to factor the trinomial x ²– 5x + 6, we can find two numbers whose product is 6 and whose sum is -5. These numbers are -2 and -3, so we can factor the trinomial as (x – 2)(x – 3).

Simplifying Polynomials with More Than Three Terms

Polynomials with more than three terms can be factored by grouping terms with common factors. For example, to factor the polynomial x ³– 2x ²+ 5x – 10, we can group the first two terms and the last two terms:

(x ³– 2x ²) + (5x – 10)

Factoring out the common factors x ²and 5, respectively, we get:

x ²(x – 2) + 5(x – 2)

Finally, we can factor out the common factor (x – 2) to obtain the simplified polynomial:

(x – 2)(x ²+ 5)

Applications in Mathematics

Polynomials have wide applications in different areas of mathematics. They are used to model and solve problems in algebra, geometry, calculus, and other branches of mathematics.

In algebra, factoring polynomials is used to simplify expressions, solve equations, and find roots. For example, factoring a quadratic polynomial of the form $ax^2+bx+c$ can be used to find its roots using the quadratic formula.

Geometry

In geometry, polynomials are used to represent the areas and volumes of geometric shapes. For example, the area of a rectangle can be represented by the polynomial $x\times y$, where $x$ and $y$ are the lengths of the sides. Similarly, the volume of a rectangular prism can be represented by the polynomial $x\times y\times z$, where $x$, $y$, and $z$ are the lengths of the three sides.

Calculus

In calculus, polynomials are used to represent the derivatives and integrals of functions. The derivative of a polynomial is a polynomial of one degree less, and the integral of a polynomial is a polynomial of one degree higher. These properties are used to find the slopes of curves and the areas under curves, respectively.

Graphical Representations

Factored polynomials can be represented graphically to visualize their behavior and characteristics. By plotting the individual factors of a polynomial, we can gain insights into its roots, extrema, and overall shape.

To graph a factored polynomial, we can use a coordinate plane and plot the graphs of each factor separately. The points where these graphs intersect the x-axis represent the roots of the polynomial.

Example: Graphing a Factored Polynomial

Consider the polynomial f(x) = (x – 2)(x + 1). We can graph this polynomial by plotting the graphs of its factors y = x – 2 and y = x + 1.

• The graph of y = x – 2 is a line with a y-intercept of -2 and a slope of 1.
• The graph of y = x + 1 is a line with a y-intercept of 1 and a slope of 1.

Plotting these graphs on a coordinate plane, we see that they intersect at the points x = 2 and x = -1. These points represent the roots of the polynomial f(x) = (x – 2)(x + 1).

Historical Development

Polynomial factorization, a fundamental technique in algebra, has a rich history marked by the contributions of brilliant mathematicians over centuries.

The earliest known attempts at polynomial factorization can be traced back to ancient civilizations like Babylon and Egypt. Babylonian mathematicians used geometric methods to solve quadratic equations, while Egyptian mathematicians employed an intuitive approach to factorize polynomials.

Early Mathematicians

In the 3rd century BC, the Greek mathematician Euclid developed a method for finding the greatest common factor (GCF) of two polynomials, which laid the foundation for polynomial factorization. In the 9th century AD, the Persian mathematician Al-Khwarizmi introduced the concept of completing the square, a technique used to factorize quadratic polynomials.

Renaissance and Enlightenment

During the Renaissance, Italian mathematician Luca Pacioli (1445-1517) developed a method for factorizing cubic polynomials. In the 17th century, French mathematician François Viète (1540-1603) introduced the use of variables in polynomial equations, which greatly simplified factorization.

19th and 20th Centuries

The 19th century witnessed significant advancements in polynomial factorization. Irish mathematician William Rowan Hamilton (1805-1865) developed a method for factorizing quartic polynomials, while Norwegian mathematician Niels Henrik Abel (1802-1829) proved the impossibility of solving quintic and higher-degree polynomials by radicals.

In the 20th century, the development of computer algebra systems revolutionized polynomial factorization. These systems allowed for efficient factorization of polynomials of very high degrees, opening up new avenues for research and applications.

FAQ Overview

What is the significance of factoring polynomials?

Factorization simplifies complex polynomials, making them easier to analyze and manipulate. It facilitates equation solving, expression simplification, and the study of polynomial functions.

How can factored polynomials be used to solve equations?

By setting each factor of a factored polynomial equal to zero, we can determine the roots or solutions of the original equation. This approach simplifies equation solving, especially for higher-degree polynomials.

What are some real-world applications of polynomial factorization?

Factorization finds applications in engineering, physics, computer science, and economics. For instance, it is used in circuit analysis, projectile motion modeling, data compression, and financial forecasting.