Welcome to our comprehensive guide on solving linear systems by substitution worksheet answers. This guide is designed to provide you with a deep understanding of the concept, step-by-step instructions, and real-world applications. Whether you’re a student looking to master this technique or a professional seeking to refresh your knowledge, this guide has everything you need.
In this guide, we will explore the concept of solving linear systems by substitution, provide a sample worksheet with detailed solutions, offer practice problems with answer keys, and discuss the importance of this technique in various fields.
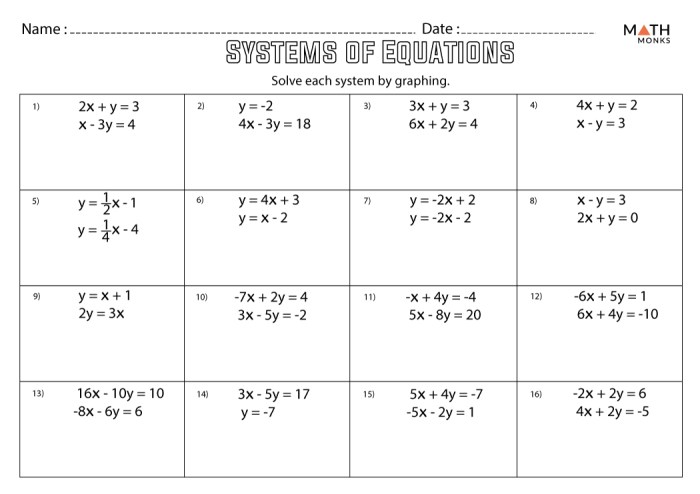
Solving Linear Systems by Substitution
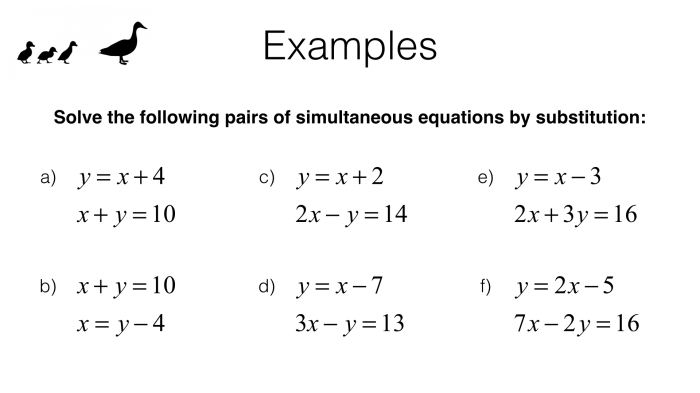
Substitution is a method for solving systems of linear equations by solving one equation for a variable and then substituting that expression into the other equation.
Linear systems that can be solved using substitution are those where one of the variables can be easily isolated in one of the equations.
Steps Involved in Solving Linear Systems by Substitution
- Solve one of the equations for one of the variables.
- Substitute the expression for that variable into the other equation.
- Solve the resulting equation for the other variable.
- Substitute the value found in step 3 back into one of the original equations to find the value of the first variable.
Worksheet Answers, Solving linear systems by substitution worksheet answers
Worksheet Problem 1: Solve the following system of equations: “` 2x + y = 10 x – y = 2 “`
Solution: 1. Solve the second equation for y: “` x – y = 2 y = x – 2 “`
2. Substitute the expression for y into the first equation: “` 2x + (x – 2) = 10 3x = 12 x = 4 “`
3. Substitute the value of x back into the second equation to find y: “` 4 – y = 2 y = 2 “`
Therefore, the solution to the system of equations is (x, y) = (4, 2).
Practice Problems
Easy
- Solve the following system of equations: “` x + y = 5 x – y = 1 “`
- Solve the following system of equations: “` 2x + 3y = 10 x – y = 1 “`
Medium
- Solve the following system of equations: “` 3x + 2y = 11 x – 3y = 1 “`
- Solve the following system of equations: “` 2x + 5y = 10 3x – 2y = 1 “`
Hard
- Solve the following system of equations: “` 4x + 3y – 2z = 1 2x – y + z = 5 x + 2y – 3z = 2 “`
- Solve the following system of equations: “` 3x – 2y + 4z = 10 x + y – 2z = 1 2x + 3y – z = 5 “`
Applications
Solving linear systems by substitution is useful in a variety of real-world applications, including:
- Finding the point of intersection of two lines.
- Solving systems of equations in science and engineering.
- Solving systems of equations in everyday life, such as calculating the cost of items or the distance traveled.
Being able to solve linear systems by substitution is an important skill for students and professionals in a variety of fields.
Essential Questionnaire: Solving Linear Systems By Substitution Worksheet Answers
What is the substitution method for solving linear systems?
The substitution method involves solving one equation for one variable and substituting that expression into the other equation to solve for the remaining variable.
What types of linear systems can be solved using substitution?
Linear systems with two equations and two variables, where one equation can be easily solved for one variable, are suitable for the substitution method.
What are some real-world applications of solving linear systems by substitution?
Solving linear systems by substitution finds applications in various fields, such as calculating the intersection point of two lines, determining the break-even point in business, and solving mixture problems in chemistry.